Hanniverse！
0%

【AML】Linear Models for Classification

Posted on Edited on In

Logistics Regression

逻辑回归虽然被称为回归，本质上其实是分类模型了，常用于二分类。逻辑回归假设数据服从伯努利分布(因为是二分类),通过极大似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

  • 决策函数：设x是m维的样本特征向量(input)；y是标签label，为正例和负例。 则该样本是正例的概率为：

p(y=1∣x)=11+e−(wTX+b) p(y=1 | x) = \frac{1}{1+e^{-(w^TX+b)}}

这里使用sigmoid函数的目的是为了把普通的线性回归问题转化为输出为[0,1]区间的二分类问题。

  • 损失函数&极大似然估计：

假设样本的概率取值可以表示为：

p(y=1∣x)=p(x),p(y=0∣x)=1−p(x)p(y=1 | x) = p(x), p(y =0|x) = 1-p(x)

因此似然函数可以表示为

L(w)=Πi=1np(xi)yi(1−p(xi))1−yiL(w) = \Pi_{i=1}^n p(x_i)^{y_i} (1-p(x_i))^{1-y_i}

对数似然函数：

logL(w)=∑i=1n(yilog(p(xi))+(1−yi)log(1−p(xi)))=∑i=1n(yi(wxi+b)−log(1+ewxi+b))logL(w) = \sum_{i=1}^n ({y_i} log(p(x_i)) + ({1-y_i})log(1-p(x_i))) \\ = \sum_{i=1}^n ({y_i} (wx_i+b) - log(1+ e^{wx_i+b}))

因此，逻辑回归的损失函数可以表示为：

J(w)=−1nlogL(w)J(w) = -\frac{1}{n} logL(w)

即在逻辑回归模型中，我们最大化似然函数和最小化损失函数实际上是等价的。

  • 正则化逻辑回归
    和线性回归一样，逻辑回归的损失函数也可以加上正则化项：
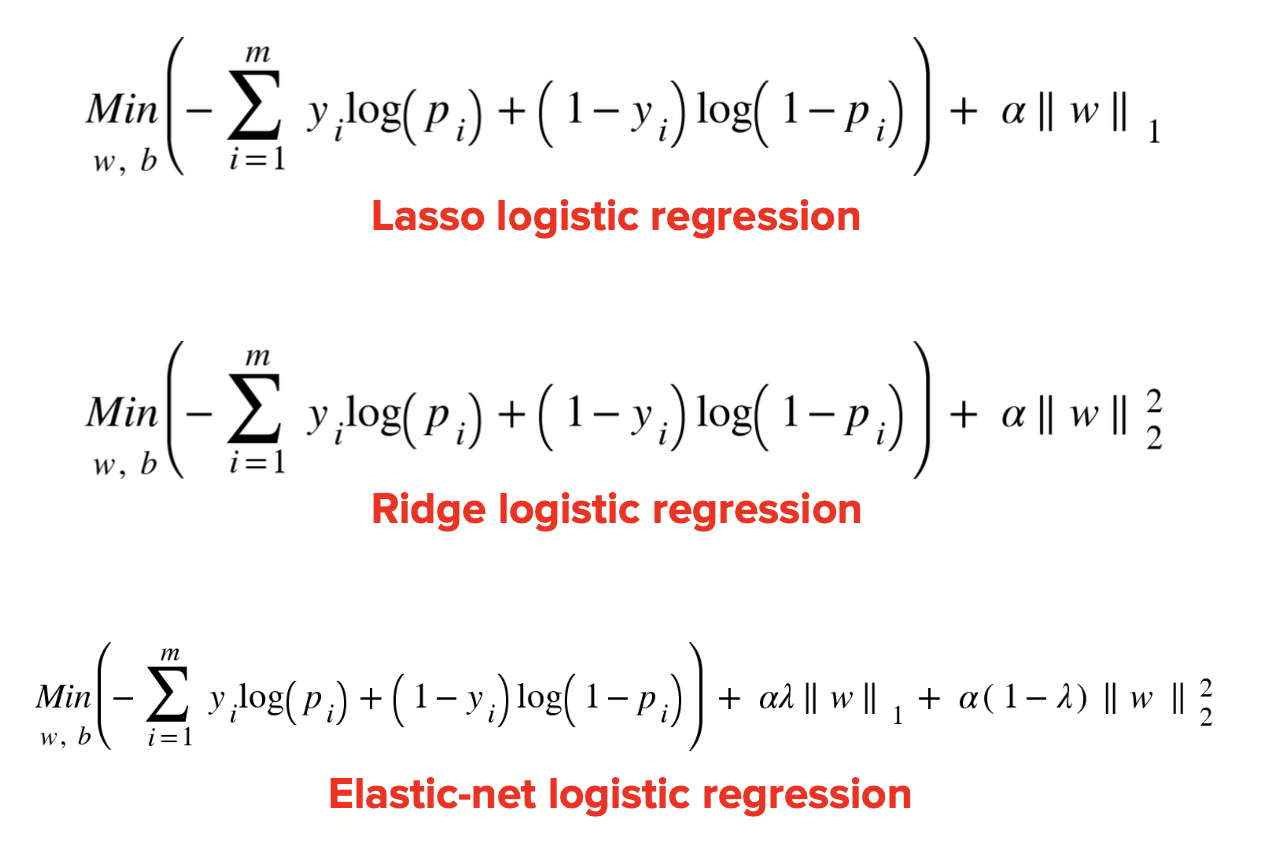
    image.png

  • 逻辑回归与线性回归的联系与区别：
    逻辑回归和线性回归首先都是广义的线性回归，区别在于逻辑回归多了个Sigmoid函数，使样本映射到[0,1]之间的数值，从而来处理分类问题。除Sigmoid函数映射关系外，其他的算法都是线性回归的。

逻辑回归是假设变量服从伯努利分布，线性回归假设变量服从高斯分布。逻辑回归输出的是离散型变量，用于分类，线性回归输出的是连续性的，用于预测。逻辑回归是用最大似然法去计算预测函数中的最优参数值，而线性回归是用最小二乘法去对自变量量关系进行拟合。

  • 逻辑回归在训练的过程当中，如果有很多的特征高度相关，或者说有一个特征重复了100遍，会造成怎样的影响？
    如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。可以认为这100个特征和原来那一个特征扮演的效果一样，只是可能中间很多特征的值正负相消了。 但去掉相关项会让模型的可解释性增强，并且可以提升训练速度。

Support Vector Machines(SVM)

在二维平面上，对两类点进行线性分割，以求两类点的边缘之间有最大的间隔。因此，其实只需要考虑两类点集的边缘上的点，即为主要参与决策的点。这些点就是SVM所说的Support Vector，用以支持分类的支持向量。引申到高位空间，直线被替换为超平面，在该平面上面的被分为正例，在该平面下面的被分为负例。两个点集合边缘的超平面之间的距离即为margin，而SVM算法的目标即是在所有点都被正确分类的前提下，最大化margin的取值。

Hard-margin & Soft-margin

对于线性可分的训练集，可以找到超平面使得两分类完全可分。数学表达为：

minw,b12∣∣w∣∣22min_{w,b} \frac{1}{2}||w||_2^2

s.t.  yi(wTxi+b)≥1,yi∈{−1,1}s.t. \ \ y_i(w^Tx_i + b) \geq 1, y_i \in \{-1,1\}

目标为求解w,bw,b，使用拉格朗日法进行求解。转化后的拉格朗日函数将为凸函数，因此也可以利用对偶问题进行求解。可以注意到原问题落在n×nn\times n的特征空间内，而对偶问题将落在m×mm\times m的样本空间内，因此当出现n远大于m时，使用对偶问题求解会简化问题，反之亦然。

Hard Margin的对偶问题最终解

αi(1−yi(wTxi+b))=0\alpha_i (1- y_i(w^Tx_i + b )) = 0

可以注意到，只有当样本点落在超平面上时，αi\alpha_i 才会取非零值。落在超平面上的点即为支持向量，最终的prediction由所有支持向量结合ww,bb得出：

pred=sign(∑iαiyi(x⋅xi)+b)pred = sign(\sum_i\alpha_iy_i(x\cdot x_i) +b)

与逻辑回归和线性回归相比，SVM得出的模型会包含训练集中的支持向量值。

在线性不可分的情况下，总会有一些点被错误的分类。于是可以在损失函数中加入了对错误分类的惩罚

minw,b12∣∣w∣∣22+C(penalty for error)min_{w,b} \frac{1}{2}||w||_2^2 + C (penalty \ for \ error)

修改之后的损失函数和逻辑回归十分相似，

损失函数中的C为超参数，可以根据实际情况进行调整。

在线性不可分情况下，支持向量(αi>0\alpha_i>0)包括落在边界上的，和落在两个分类边界之间的，以及分类错误的。

Kernel-SVM

在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。如将二维空间中无法划分的数据映射到三维空间便可以找到分离超平面。

  • 函数ϕ(x)\phi(x)可以将数据映射到高维空间
  • 计算两个向量在隐式映射过后的空间中的内积的函数为核函数K(xi,xj)K(x_i,x_j)

Kernel Trick: 当核函数对称并且正定，必能找到对应的ϕ(x)\phi(x)使得$$K(x_i,x_j) = \phi(x_i)^T\phi(x_i)$$
在此条件下，可以直接定义核函数而不用显式定义出ϕ(x)\phi(x).

常见的核函数：

Multi-class classification

  • OVR (one vs rest): n 种类型的样本进行分类时，分别取一种样本作为一类，将剩余的所有类型的样本看做另一类，这样就形成了 n 个二分类问题，使用逻辑回归算法对 n 个数据集训练出 n 个模型，将待预测的样本传入这 n 个模型中，所得概率最高的那个模型对应的样本类型即认为是该预测样本的类型。

  • OVO(one vs one): n 类样本中，每次挑出 2 种类型，两两结合，一共有 Cn2C_n^2 种二分类情况，使用 Cn2C_n^2 种模型预测样本类型，有 Cn2C_n^2 个预测结果，种类最多的那种样本类型，就认为是该样本最终的预测类型。