二叉排序树
定义: 二叉排序树或者是一棵空树;或是具有如下特性的二叉树:
- 若左子树不为空,则左子树上所有节点值均小于根节点;
- 若右子树不为空,则右子树上所有节点值均大于根节点;
- 左、右子树均为二叉排序树.
核心算法: 查找算法、插入算法、删除算法
查找算法
若二叉排序树为空,则查找不成功;
否则从根节点向下查找:
- 若给定值=根节点关键字,则查找成功;
- 若给定值<根节点值关键字,则继续在左子树查找;
- 若给定值>根节点值关键字,则继续在右子树查找;
通过递归实现.
查找成功:
从根结点出发,沿着左分支或右分支逐层向下直至关键字等于给定值的结点
查找不成功:
从根结点出发,沿着左分支或右分支逐层向下直至指针指向空树为止。
插入算法
插入某元素首先要判断该元素是否已经在二叉树内,
若存在,则插入不成功;
否则从根节点向下查找插入位置:
- 若二叉排序树为空树,则新插入的结点为新的根结点;
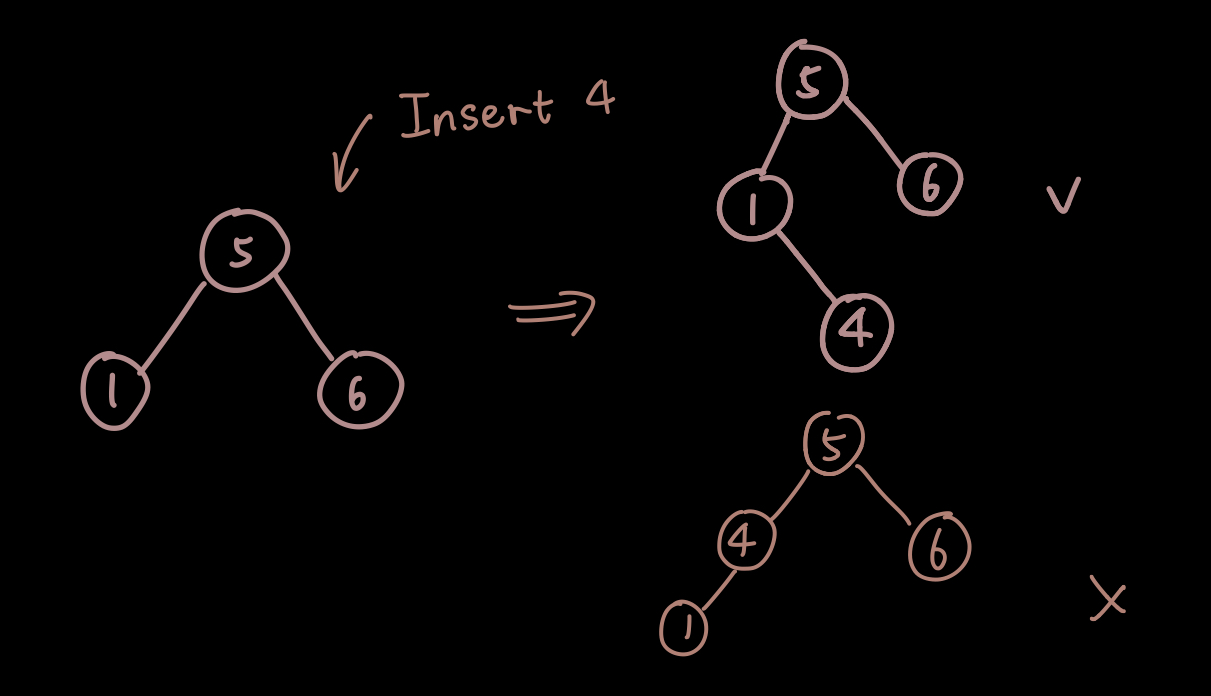
- 若不为空,找到查找算法中返回的最后一个父节点的位置,若插入元素值>父节点值关键字,则成为其右子树;若小于则为左子树
**Notice:**插入顺序优先于元素值的排序,for example
删除算法
和插入相反,删除在查找成功之后进行,并且要求在删除二叉排序树上某个结点之后,仍然保持二叉排序树的特性。
首先判断需删除的元素是否在二叉树内,
若不存在,则删除不成功;
否则需要分情况处理删除后的二叉排序树:
- 若被删元素所在节点为叶节点(左右子树均为空),直接删除该元素即可;
- 若被删元素所在节点仅有左子树/仅有右子树,则需要将其子树接在父节点的位置;
**Notice:**需要判断删除元素所在子树为父节点的哪一支,之后在1中对父节点的该子树置空,在2中将其子树接在父节点的对应空子树位置(会出现删除节点为父节点的左子树,但其遗留子树为“右子树”的情况,不要搞混了)
-
关键情形:被删除元素所在节点既有左子树,也有右子树
(1)首先通过中序遍历找到其前驱节点;(遍历方法同二叉树)
(2)删除前驱节点后以前驱节点的值替代该节点(递归)
算法实现
- 实现类同二叉树,使用Node保存节点信息(排序树中可定义值(key)为排序关键字,data存储需要被排序/搜索的信息)
- 搜索算法中使用额外构建
Node[] 用于保存递归结束时得到的父节点,方便进行插入和删除操作
**Problem:**根据操作序列构造二叉排序树,输出二叉排序树的前序遍历序列和中序遍历序列。
Input:
第一个整数n表示操作的个数,接下来每一个行代表一个操作。
对于每行的第一个字符,I表示插入,D表示删除,第二个数字表示的是操作数。
例如,I 2表示往二叉排序树中插入2,D 3表示从二叉排序树中删除3。
注意:插入的数字可能已经存在树中,而删除的数字也可能不存在树中。
| Sample Input |
Output |
5
I 5
I 3
I 6
I 2
D 3 |
5 2 6
2 5 6 |
实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
| import java.util.Scanner;
class Node{
public int key;
public Node lchild;
public Node rchild;
}
public class BinarySearchTree {
public Node root=null;
public Node Search(int key, Node node, Node father,Node[] record){
if(node ==null){
record[0]=null;
record[1]=father;
return null;
}
if(node.key ==key){
record[0] = node;
record[1] = father;
return node;
}
if(node.key<key){
return Search(key,node.rchild,node,record);
}
else{
return Search(key,node.lchild,node,record);
}
}
public boolean Insert(int key) {
if (root == null) {
root = new Node();
root.key = key;
root.lchild = null;
root.rchild = null;
return true;
} else {
Node[] rec = new Node[2];
Node present = Search(key, root, null, rec);
if (present != null) {
return false;
} else {
Node node = new Node();
node.key = key;
node.lchild = null;
node.rchild = null;
if (node.key > rec[1].key) {
rec[1].rchild = node;
} else {
rec[1].lchild = node;
}
return true;
}
}
}
private static String preOrder(Node node){
if(node == null){
return "";
}
else{
String str = node.key + " ";
str += preOrder(node.lchild);
str += preOrder(node.rchild);
return str;
}
}
public String preOrder(){
return preOrder(root);
}
private static String inOrder(Node node){
if(node == null){
return "";
}
else{
String str = inOrder(node.lchild);
str += node.key + " ";
str += inOrder(node.rchild);
return str;
}
}
public String inOrder(){
return inOrder(root);
}
public boolean delete(int key){
if(root ==null){
return false;
}
else{
Node[] rec = new Node[2];
Node present = Search(key, root, null, rec);
if (present == null) {
return false;
} else {
if(present.lchild ==null && present.rchild ==null){
if(rec[1] == null){
root = null;
} else {
if(present.key<rec[1].key) rec[1].lchild = null;
else{
rec[1].rchild = present.lchild;
}
}
present = null;
return true;
}
if(present.lchild!=null && present.rchild==null){
if(rec[1] ==null){
root = present.lchild;
return true;
}
if(present.key<rec[1].key){
rec[1].lchild = present.lchild;
return true;
}
else{
rec[1].rchild = present.lchild;
return true;
}
}
if(present.lchild==null && present.rchild!=null){
if(rec[1] ==null){
root = present.rchild;
return true;
}
if(present.key<rec[1].key){
rec[1].lchild = present.rchild;
return true;
}
else{
rec[1].rchild = present.rchild;
return true;
}
}
else{
String inorder = inOrder(root);
String[] ino = inorder.split(" ");
int prior=0;
for(int i=0;i< ino.length;i++){
if(Integer.parseInt(ino[i])== present.key){
prior = Integer.parseInt(ino[i-1]);
}
}
boolean tt=delete(prior);
present.key = prior;
return tt;
}
}
}
}
public static void main(String[] args){
Scanner sc= new Scanner(System.in);
int n = sc.nextInt();
sc.nextLine();
BinarySearchTree tree = new BinarySearchTree();
for(int i=0;i<n;i++){
String str =sc.nextLine();
String[] split = str.split(" ");
String order = split[0];
int key = Integer.parseInt(split[1]);
if("I".equals(order)){
tree.Insert(key);
}
if("D".equals(order)){
tree.delete(key);
}
}
sc.close();
System.out.println(tree.preOrder());
System.out.println(tree.inOrder());
}
}
|
